Rayleigh Scattering: Phase Function
Definitions of Angles
See Figure 11. The angle between the incident flux and the
local normal is given by  and µ0
and µ0  cos(
cos( ).
The angle between the local normal and the observer is given by
).
The angle between the local normal and the observer is given by
 and µ
and µ  cos(
cos( ). The phase angle,
). The phase angle,
 , is the angle between the incident and emission through the
origin. The azimuthal angle,
, is the angle between the incident and emission through the
origin. The azimuthal angle, 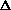
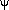 , is the projection of the
solar incidence and emission directions onto the local horizon. Using
spherical trigonometry cosine laws (e.g., see CRC pg. 146) we can
easily obtain the value of
, is the projection of the
solar incidence and emission directions onto the local horizon. Using
spherical trigonometry cosine laws (e.g., see CRC pg. 146) we can
easily obtain the value of 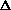
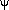 ) given µ0, µ, and
) given µ0, µ, and  . For solar scattering to an observer above the atmosphere the
angles are related by:
. For solar scattering to an observer above the atmosphere the
angles are related by:
cos( ) =
) = 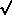 [(1-µ02)(1-µ2)] · cos(
[(1-µ02)(1-µ2)] · cos(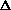
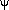 ) -/+
µ µ0 (S = +, T = -)
) -/+
µ µ0 (S = +, T = -)
This is the method employed by Chandrasekar, Liou, and others.
We could also write the equations in terms of the scattering angles.
The scattering angle between incidence and emission, 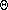 , which
is related to the phase function, is given by
, which
is related to the phase function, is given by 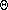 =
=  -
-  .
The scattering angle in the horizontal plane,
.
The scattering angle in the horizontal plane, 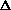
 is related
to the azimuthal angle, and is given by
is related
to the azimuthal angle, and is given by 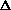
 =
=  -
- 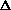
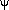 . This definition is used by Hansen, Tomasko, and Danielson.
It is the method employed within the VIAMP programs. Note the sign
change between the two methods.
. This definition is used by Hansen, Tomasko, and Danielson.
It is the method employed within the VIAMP programs. Note the sign
change between the two methods.
cos(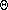 ) =
) = 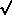 [ (1-µ02)(1-µ2)] · cos(
[ (1-µ02)(1-µ2)] · cos(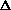
 ) ±
µ µ0 (T = +, S = -)
) ±
µ µ0 (T = +, S = -)
The Rayleigh phase function is given in terms of scattering angles or phase angles by
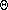 ) = (3/4) (1 + cos2(
) = (3/4) (1 + cos2(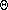 )) = (3/4)(1 + cos2(
)) = (3/4)(1 + cos2( )) = Pray(
)) = Pray( )
)
The cos2 term can be expressed in terms of
µ, µ0, and 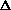
 as
as
cos2(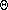 ) = (1-µ02)(1-µ2) · cos2(
) = (1-µ02)(1-µ2) · cos2(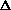
 )
± 2µµ0
)
± 2µµ0 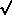 [ (1-µ02)(1-µ2) ] · cos(
[ (1-µ02)(1-µ2) ] · cos(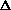
 )
+ (µ2 µ02)
)
+ (µ2 µ02)
cos(2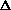
 ) = 2 cos2(
) = 2 cos2( ) - 1 or,
) - 1 or,
 ) = 1/2 cos(2
) = 1/2 cos(2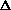
 ) + 1/2
) + 1/2
cos2(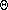 ) = 1/2 (1-µ02)(1-µ2) · cos(2
) = 1/2 (1-µ02)(1-µ2) · cos(2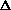
 )
±
2 µ µ0
)
±
2 µ µ0 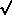 [ (1-µ02)(1-µ2) ] · cos(
[ (1-µ02)(1-µ2) ] · cos(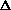
 )
+
µ2 µ02 + 1/2 (1-µ02)(1-µ2)
)
+
µ2 µ02 + 1/2 (1-µ02)(1-µ2)
So the Rayleigh phase function can be written in terms of 3 Fourier moments:
Pray(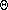 ) = P1 + P2 cos(
) = P1 + P2 cos(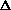
 ) + P3 cos(2
) + P3 cos(2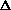
 )
)
P0 = 3/4 [ 1 + µ2 µ02 + 1/2 (1-µ02)(1-µ2) ] = 3/8 ( 3 + 3 µ2 µ02 -µ02 -µ2 )
P1 = ± 3/2 ( µ µ0
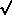 [(1-µ02)(1-µ2)] ) (T = +, S = -)
[(1-µ02)(1-µ2)] ) (T = +, S = -)
P2 = 3/8 (1-µ02)(1-µ2)
 PDS: The Planetary Atmospheres Node
PDS: The Planetary Atmospheres Node
