Amagats


From the ideal gas law we can define the number of particles at standard temperature (273.15 K) and standard pressure (1 atm = 1013.25 milli-bars). The ideal gas law can be written many ways, here we will adopt the notation(s)

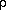P = N k T = rho Na k T/<mw> = 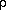rho Rg T
where, N is the number of molecules per unit volume, Boltzmann's constant k = 1.3806 · 10-16 erg/K, the gas constant
Rg = Na · k/<mw>, Avogadro's number, Na = 6.02 · 1023 particles per mole, <mw> is the molecular weight in grams/mole.
This number of molecules at STP is called Loschmidt's number and has the value,
N0 = Pstp/(k · Tstp) = 2.687 · 1019 cm-3

The number of amagats of a gas is given as a ratio of the actual number of particles at the given temperature and pressure to Loschmidt's number. In planetary atmospheres the number density is a function of height. We can calculate the thickness of an equivalent atmospheric column at standard temperature and pressure. This is denoted as cm-amagats or Km-amagats and is given by

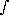Z = (1/N0) integ Ni(z) · dz
Hydrostatic equilibrium relates the pressure and vertical coordinates
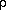dP ident - rho g dz, or dz = -dP/(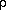rho g),
and the number density, Ni can be written as a function of the density,
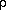Ni = qi · rho Na/<mw>, molecules/cm3
where, qi is the volumetric fraction of species i.
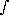Z = Na/(g N0) integ qi/<mw> · dP 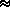approx Na/(g N0) · ( qi/<mw>) · P = H0 · P
H0 = 10 · Na qi/(g N0 <mw>) Km-amagat/Bar

EarthMarsJupiterSaturnTitanUranusNeptune
g981.0374.12425.31000.0136.0880.11110.5 cm/s
q(H2)1.001.000.900.961.000.850.85
<mw>28.9744.012.222.1428.002.302.30 gm/mole
H07.8813.6137.45100.5058.8594.0874.56 Km-am/Bar
1000/H0126.973.4926.709.9516.9910.6313.41 mB/Km-am