Planck function
The Planck function, B (T), is given by
(T), is given by (T) = (
(T) = ( 1
1  3)/[exp(
3)/[exp( 2
2  /T) - 1]
/T) - 1]where,
 = wavenumber in cm-1 = 104/
= wavenumber in cm-1 = 104/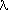 ,
, 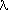 in µm.
in µm. 1 = 2 h c2 = 1.191066 · 10-5 for radiance in units of
mW · m-2 · steradian-1/cm-1.
1 = 2 h c2 = 1.191066 · 10-5 for radiance in units of
mW · m-2 · steradian-1/cm-1. 2 = h c / k = 1.438833 K cm
2 = h c / k = 1.438833 K cm is the Stefan-Boltzmann constant = 5.67 · 10-5 erg · s-1 · cm-2 · K-4
or mW · m-2 · K-4
is the Stefan-Boltzmann constant = 5.67 · 10-5 erg · s-1 · cm-2 · K-4
or mW · m-2 · K-4
 · T4
· T4
The brightness temperature, Tb, of a given radiance, R ,
is found with the inverse of the Planck function.
,
is found with the inverse of the Planck function.
 B-1
B-1 (R
(R ) = (
) = ( 2 ·
2 ·  )/
loge [ 1 + (
)/
loge [ 1 + ( 1
1  3/R
3/R ) ]
) ]
The derivative of the Planck function is given by
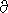 B
B /
/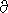 T =
(
T =
( 1
1  2
2  4/T2) ·
exp(
4/T2) ·
exp( 2
2  /T)/[exp(
/T)/[exp( 2
2  /T) - 1]2
/T) - 1]2
Infrared approximation: for 
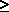 600 cm-1 and
T
600 cm-1 and
T  300 K.
300 K.
 (T)
(T) 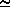
 1
1  3 exp(-
3 exp(- 2
2  /T)
mW · m-2 · steradian-1/cm-1
/T)
mW · m-2 · steradian-1/cm-1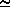 (-
(- 2 ·
2 ·  )/ loge [ (
)/ loge [ ( 1
1  3/R
3/R ) ]
) ]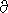 B
B /
/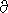 T
T 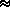 (
( 1
1  2
2  4)/T2 · exp[-
4)/T2 · exp[-  2
2  /T]
/T]
Microwave Rayleigh Jeans approximation: 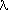 (mm) =
300/f,
(mm) =
300/f,  = f/30 cm-1, f is in GHz
= f/30 cm-1, f is in GHz
Wavenumbers,  , are frequency units and are assumed to be in
vacuum while wavelength is the wavelength specified within the
medium. Typically, wavelengths are expressed as wavelength in air,
, are frequency units and are assumed to be in
vacuum while wavelength is the wavelength specified within the
medium. Typically, wavelengths are expressed as wavelength in air,
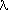 a or wavelength in vacuum,
a or wavelength in vacuum, 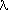 v.
v.

 10000/
10000/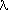 v
v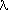 v = na ·
v = na · 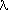 a
a = 10000/(na ·
= 10000/(na · 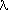 a) na = 1.00027
a) na = 1.00027
| f | cm-1 | µm | mm | |
| 0.66 GHz | 0.02 | 454545 | 454.55 | P band (SAR) |
| 1.25 GHz | 0.04 | 240000 | 240.00 | C band (SAR) |
| 5.33 GHz | 0.18 | 56285 | 56.29 | L band (SAR) |
| 6.6 GHz | 0.22 | 45454 | 45.45 | MIMR (surface) |
| 23 GHz | 0.77 | 13043 | 13.04 | AMSU-A |
| 50 GHz | 1.67 | 6000 | 6.00 | AMSU-A |
| 60 GHz | 2.00 | 5000 | 5.00 | AMSU-A |
| 89 GHz | 2.97 | 3371 | 3.37 | AMSU-C |
| 118 GHz | 3.93 | 2542 | 2.54 | MHS-X |
| 183 GHz | 6.10 | 1639 | 1.64 | AMSU-B |

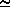
 1/(
1/( 2 · c2 · 10-18) · f2 · T
= 9.2105 · 10-9 · f2 · T mW · m-2 · steradian-1 ·/cm-1
2 · c2 · 10-18) · f2 · T
= 9.2105 · 10-9 · f2 · T mW · m-2 · steradian-1 ·/cm-1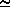 1.0857 · 108 R
1.0857 · 108 R /f2
/f2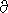 B
B /
/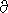 T
T 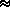 2 · c · k ·
2 · c · k ·  2 =
2 =  1/
1/ 2 ·
2 ·  2
=
2
=  1/(
1/( 2 · c2 · 10-18) · f2
2 · c2 · 10-18) · f2
| wavelength mm | frequency GHz | B(T=300K) mW/m2/ster/cm-1 | dB/dT mW/m2/ster/cm-1/K | (1/B) · dB/dT %/K |
| 6.0 | 50 | 0.007 | 0.000023 | 0.335 |
| 3.0 | 100 | 0.027 | 0.000092 | 0.336 |
| 2.0 | 150 | 0.061 | 0.000207 | 0.337 |
| 1.5 | 200 | 0.109 | 0.000368 | 0.338 |
| wavelength µm | wavenumber cm-1 | B(T=300K) mW/m2/ster/cm-1 | dB/dT mW/m2/ster/cm-1/K | (1/B) · dB/dT %/K |
| 16.7 | 600 | 153.38 | 1.559 | 1.0 |
| 9.1 | 1100 | 81.49 | 1.441 | 1.8 |
| 6.2 | 1600 | 22.69 | 0.581 | 2.6 |
| 4.3 | 2300 | 2.35 | 0.086 | 3.7 |
| 3.7 | 2700 | 0.56 | 0.024 | 4.3 |
| 3.3 | 3000 | 0.18 | 0.009 | 4.8 |
 PDS: The Planetary Atmospheres Node
PDS: The Planetary Atmospheres Node
