Equations of Motion
Momentum
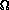 x V -
(1/
x V -
(1/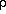 )
) 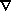 P + k g + F
P + k g + F i u + j v + k w
i u + j v + k w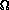 v sin(
v sin( ) =
(-1/
) =
(-1/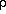 ) (
) (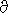 P/
P/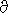 x)
+ (u v tan(
x)
+ (u v tan( )/a) - (u w/a)
- 2
)/a) - (u w/a)
- 2 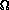 w cos(
w cos( ) + Fx
) + Fx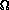 u sin(
u sin( ) =
(-1/
) =
(-1/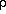 ) (
) (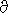 P/
P/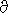 y)
- (u2 tan(
y)
- (u2 tan( )/a) - (v w/a) + Fy
)/a) - (v w/a) + Fy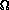 u cos(
u cos( ) =
(-1/
) =
(-1/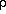 ) (
) (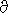 P/
P/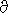 z)
+ ((u2 + v2)/a) - g + Fz
z)
+ ((u2 + v2)/a) - g + FzContinuity
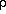 ) (d
) (d 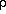 /dt) +
/dt) +
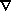 · V = 0
· V = 0when motions are on the order of a scale height or less
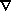 · (
· (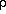 0V) = 0
0V) = 0Energy
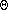 )/dt) =
(cp/T) (dT/dt) -
(Runiv/P) (dP/dt)
)/dt) =
(cp/T) (dT/dt) -
(Runiv/P) (dP/dt) PDS: The Planetary Atmospheres Node
PDS: The Planetary Atmospheres Node
