Rayleigh Scattering: Optical Depth
The average scattering cross section per particle is given by
 (
( ) = (128
) = (128  5
5  2)/(3
2)/(3  4)
· [ (6 + 3
4)
· [ (6 + 3 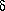 )/(6 - 7
)/(6 - 7 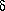 ) ]
) ] = (n - 1)/(2
= (n - 1)/(2  N0)
N0) 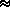 (n2 - 1)/(4
(n2 - 1)/(4  N0), for n near unity
N0), for n near unity
where, n is the index of refraction, N0 is the number of
molecules per unit volume at standard temperature and pressure (
i.e., conditions of index of refraction), 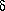 is the
depolarization factor.
is the
depolarization factor.
The optical depth can be related to the ``thickness'' of the atmosphere. If Z is the thickness in Km-amagats then:
 ray(
ray( ) =
) = 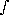 N(z) ·
N(z) ·  (
( ) dz
) dz 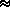
 (
( ) ·
) · 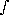 N(z) · dz =
Z · N0 ·
N(z) · dz =
Z · N0 ·  (
( )
)
The index of refraction has a wavelength dependence. This is usually represented by two constants, A and B, as follows:
(n-1) = A · (1 + B/ 2),
2),  in µm
in µm
(n-1)2 = A2 · (1 +
2 B/ 2 +
B2/
2 +
B2/ 4)
4)
 ray = Z a0/
ray = Z a0/ 4
· (1 + a1/
4
· (1 + a1/ 2 + a2/
2 + a2/ 4) where,
4) where,
a0 = (32  3)/(3 N02) ·
[(6 + 3
3)/(3 N02) ·
[(6 + 3 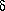 )/(6 - 7
)/(6 - 7 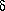 ) ] ·
) ] ·
 qi · A2
qi · A2
a1 =  qi · 2 B, and
a2 =
qi · 2 B, and
a2 =  qi · B2
qi · B2
 ray(H2) =
Z · 2.19 · 10-4/
ray(H2) =
Z · 2.19 · 10-4/ 4 ·
( 1 + 0.0157248/
4 ·
( 1 + 0.0157248/ 2 +
0.0001978/
2 +
0.0001978/ 4 ),
4 ),  in µm
in µm
The wavelength dependence in the VIAMP code is taken from
Dalgarno and Williams (ApJ, 1962). This equation is similar to the
equation above, however, it differs in the  8 term.
8 term.
 ray(H2) =
(8.14 · 10-13/
ray(H2) =
(8.14 · 10-13/ 4 +
1.28 · 10-6/
4 +
1.28 · 10-6/ 6 +
1.61/
6 +
1.61/ 8) cm2,
8) cm2,  in Å
in Å
The optical depth per Km-amagat of hydrogen, denoted by
 1(H2), is then
1(H2), is then
 1(H2) = 2.687 · 1024 ·
1(H2) = 2.687 · 1024 ·  ray(H2) =
2.687
(8.14 · 1011/
ray(H2) =
2.687
(8.14 · 1011/ 4 +
1.28 · 1018/
4 +
1.28 · 1018/ 6 +
1.61 · 1024/
6 +
1.61 · 1024/ 8),
8),  in Å
in Å
 1(H2) =
2.687
(8.14 · 10-21 f4 +
1.28 · 10-30 f6 +
1.61 · 10-40 f8), f = 108/
1(H2) =
2.687
(8.14 · 10-21 f4 +
1.28 · 10-30 f6 +
1.61 · 10-40 f8), f = 108/ and
and  in Å
in Å
And the total optical depth for a mixture of gases is given as
 ray =
ray =  1(H2) ·
1(H2) ·  Zi · [ (ni - 1)2 / (nH2 - 1)2 ]
Zi · [ (ni - 1)2 / (nH2 - 1)2 ]
Note that this formulation always uses the wavelength dependence of hydrogen, even if other gases are used.
(n-1) = A · (1 + B/ 2),
2),
 in µm
in µm
ray = (n-1)2/(nH2 - 1)2
| ray | n | A (10-5) | B (10-3) |  (10-24) | 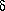 | a0 µm4/Km | |
| air | 4.4459 | 1.0002918 | 28.71 | 5.67 | 3.40 | 0.031 | 10.7E-4 |
| H2 | 1.0000 | 1.0001384 | 13.58 | 7.52 | 1.61 | 0.02 | 2.35E-4 |
| He | 0.0641 | 1.0000350 | 3.48 | 2.30 | |||
| O2 | 3.8634 | 1.000272 | 26.63 | 5.07 | 0.054 | ||
| N2 | 4.6035 | 1.000297 | 29.06 | 7.7 | 3.44 | 0.030 | 10.9E-4 |
| H2O | 3.3690 | 1.000254 | |||||
| CO2 | 10.5611 | 1.0004498 | 43.9 | 6.4 | 0.09 | ||
| CO | 5.8247 | 1.000334 | 32.7 | 8.1 | |||
| NH3 | 7.3427 | 1.000375 | 37.0 | 12.0 | |||
| NO | 4.6035 | 1.000297 | 28.9 | 7.4 | |||
| CH4 | 10.1509 | 1.000441 |
The depth of penetration of Rayleigh scattering is computed for various objects using the data above. A summary of the characteristics of the plots in Figure 9 is given below (g is gravity in cm/s2, µ = molecular weight in gm/mole, Z = KM-amagats per Bar).
| wave(µm): | 0.1000 | 0.2000 | 0.2640 | 0.3000 | 0.4000 | 0.5000 |
 (P0): (P0): | 209.57 | 6.95 | 2.05 | 1.19 | 0.36 | 0.14 |
P( =1): =1): | 4.8 | 145.7 | 493.2 | 851.0 | 2834.7 | 7094.5 |
| wave(µm): | 0.1000 | 0.2000 | 0.2640 | 0.3000 | 0.4000 | 0.5000 |
 (P0): (P0): | 299.82 | 8.62 | 2.47 | 1.42 | 0.42 | 0.17 |
P( =1): =1): | 3.3 | 116.1 | 405.2 | 706.3 | 2390.8 | 6030.4 |
| wave(µm): | 0.1000 | 0.2000 | 0.2640 | 0.3000 | 0.4000 | 0.5000 |
 (P0): (P0): | 754.31 | 21.68 | 6.21 | 3.56 | 1.05 | 0.42 |
P( =1): =1): | 1.3 | 46.1 | 161.0 | 280.7 | 950.3 | 2396.9 |
| wave(µm): | 0.1000 | 0.2000 | 0.2640 | 0.3000 | 0.4000 | 0.5000 |
 (P0): (P0): | 5378.65 | 152.59 | 43.58 | 24.98 | 7.37 | 2.92 |
P( =1): =1): | 0.3 | 9.8 | 34.4 | 60.1 | 203.6 | 513.9 |
The gas continuum absorption contains a term which is supposed
to represent the effect of Raman scattering due to the  1 vibration
of H2 at 4161 cm-1.
1 vibration
of H2 at 4161 cm-1.
Ref.: Belton et al. (1971). Atm. of
Uranus. ApJ. 164, 191-209
 raman = 0.0208 ·
raman = 0.0208 ·  ray
ray
 PDS: The Planetary Atmospheres Node
PDS: The Planetary Atmospheres Node
